1. Napisz wyrażenie określające adiabatyczne rozprężanie promieniowania:

Jeśli ciśnienie promieniowania jest opisane związkiem:  p= (1/3) – ε to: T³V = const

 

2. Sformułuj aksjomat bilansowy dla wielkości ekstensywnej.

Aksjomat bilansowy głosi, iż zmiana zasobu wielkości ekstensywnej zmagazynowanej w układzie bilansowania może być dokonana tylko bądź za przyczyną produkcji zasobu WE wewnątrz układu bilansowania, bądź za przyczyną wymiany zasobu wielkości ekstensywnej poprzez granice układu bilansowania lub w wyniku jednoczesnego przebiegu obu tych procesów.

 

3. Zdefiniuj pojęcie ciśnienia dynamicznego w poruszającym się płynie:

4. Pojemnością cieplną lub ciepłem właściwym substancji, które ozn.  literą C,

nazywamy iloraz elementarnego przyrostu masowej gęstości zasobu ciepła do elementarnego przyrostu temperatury bezwzględnej wywołanej przyrostem tego ciepła.

,

 dla gazu doskonałego C_J ,C_p= const.

 

5. Wyrażenie określające ciśnienie gazu działającego na powierzchnię padania.

Ciśnienie parcjalne na powierzchni AB: p_i =F_i/AB

Przyrost ciśnienia cząstek poruszających się z prędkością V_i w kierunku powierzchni padania pod kątem θ:

dp_i=2mV_i²cos²θdn  lub  dp_i=n_imV_i²sinθdθ

6. Zdefiniuj pojęcie wielkości ekstensywnej i podaj przykłady:

Wielkością ekstensywną (WE)nazywamy wielkość geometryczną lub fizyczną, której zasób w obszarze złożonym z sumy podobszarów równy jest sumie zasobów we wszystkich podobszarach. Przykłady wielkości wektorowych WE : pęd, kręt.

Przykłady wielkości skalarnych WE: objętość, masa, energia, entropia.

 

7. Podaj zasadę ekwipartycji energii.

Rozdział energii pomiędzy stopnie swobody tak, aby średnia energia przypadająca na każdy stopień swobody była jednakowa, nazywamy zasadą ekwipartycji energii.

 

8. Opisz zjawisko emisji wymuszonej.

Zjawisko emisji wymuszonej polega na jednoczesnym spadku wszystkich atomów znajdujących się na wyższym poziomie energetycznym na niższy poziom energetyczny. Towarzyszy temu duża ilość fotonów emitowanych o energii: hν = 2E_i tworząc spójne promieniowanie monochromatyczne o dużych gęstościach zasobu strumienia emisji energii.

 

9. Podaj klasyfikację energii układu. 

Całkowita energia układu jest równa sumie energii ruchu wszystkich cząstek substancji wypełniających układ, czyli energii kinetycznej szeroko rozumianej oraz pól siłowych w obszarze układu, czyli energii potencjalnej szeroko rozumianej.

 

10. Klasyfikacja energii wewnętrznej:

• En. ruchu postępowego i obrotowego drobin

• En. ruchu drgającego atomów w drobinach,

• En. potencjalna w polu wzajemnego, przyciągania drobin,

• En. chemiczna z możliwością przebudowy drobin,

• En. stanów elektronowych,

• En. jądrowa.

 

11. Zdefiniuj pojecie entropii i wymień inne znane ci parametry stanu gazu.

Entropia jest to zjawisko samorzutnego dochodzenia układów nie równoważonych termodynamicznie w procesach nieodwracalnych do stanu równowagi termodynamicznej.

 

12. Klasyfikacja transportu energii:

• poprzez wymianę ciepła,

• poprzez wymianę pracy,

• poprzez wymianę masy.

13. Zdefiniuj pojęcie entropii.

Entropia jest równa iloczynowi stałej Boltzmana i logarytmu gęstości prawdopodobieństwa wystąpienia stanu układu.

Ze statystycznego punktu widzenia największemu stopniu nie uporządkowania układu przyporządkowane jest największe prawdopodobieństwo wystąpienia tego stanu. Inne parametry stanu: temp. ciśnienie. Entropia izolowanego układu osiąga wartość max dla wart. zmiennej losowej X równej x odpowiadającej stanowi równowagi układu. Entropia układu złożonego z „n” słabo oddziaływujących na siebie podukładów równa jest sumie entropii tych podukładów.   

 

14. Wyrażenie na masową gęstość zasobu entropii dla gazu doskonałego.

W funkcji temp. i masowej gęstości zasobu objętości:

W funkcji temperatury i ciśnienia:

 

15. Współczynnik eustynuncji:

α_λ – współczynnik absorbcji objętości

β_α -  współczynnik rozproszenia objętości

 

16. Podział zasobu energii promieniowania:

Oznaczając zasób energii absorbowanej A, pochłoniętej P, zaś reflektowanej R, można zapisać bilans energii promieniowania padającego na ciało:

A+P+R=Q

a = A/Q – zdolność absorbcyjna

p = P/Q – zdolność przepuszczania

r = R/Q – zdolność refleksyjna

 

17. Wymień założenia przyjęte dla modelu gazu doskonałego.

-cząstki gazu mają rozmiar punktów materialnych,

-objętość zajmowana przez cząsteczki gazu jest pomijalnie mała,

-cząsteczki gazu wykazują cechy doskonale sprężystych kulek znajdujących sie w ciągłym chaotycznym ruchu prowadzącym do zderzeń miedzy sobą i ściankami naczynia; miedzy cząsteczkami gazu nie występują inne oddziaływania poza sprężystymi zderzeniami,

-bezpośrednią miarą temperatury jest średnia energia kinetyczna jego cząstek.

 

18. Określ masową gęstość zasobu ciepła dla przemiany izotermicznej:

Dla przemiany izotermicznej masowa gęstość zasobu ciepła = pracy bezwzględnej = pracy technicznej.

19. Odwracalnością termodynamiczną względem procesu termodynamicznego:

nazywamy taki stan, w którym proces termodynamiczny występujący w układzie jest w równowadze termodynamicznej, jednakże pod wpływem zadziałania elementarnego bodźca termodynamicznego przybiera kierunek przebiegu zawsze zgodny z kierunkiem zadziałania elementarnego bodźca termodynamicznego (zmiana kierunku zadziałania bodźca termodynamicznego powoduje zmianę kierunku przebiegu procesu termodynamicznego).

 

20. Praca internijna maszyny roboczej.

Jest to część pracy wykonanej wewnątrz układu ograniczonego osłoną poprowadzona wzdłuż ścian wewnętrznych maszyny, która jest przekazywana na zewnątrz układu.

L_i = L_in + L_f

L_in – praca indykatorowa równa wykresowej,

L_f – praca tarcia wewnątrz maszyny.

21. Praca odwracalnego przebiegu prawo i lewobrzeżnego:

Dla prawo: L_ob = L_ex – L_k

Dla lewo: L_obl = L_k – L_ex

Gdzie: L_ex – praca ekspansji

            L_k – praca kompresji

Dla nieodwracalnego:

L_obn = (L_ex – L_k) – (L_fex + L_fk)

L_obnl = (L_k – L_ex) – (L_fex + L_fk)

 

22. Średnia prędkość kwadratów prędkości cząsteczek w gazie doskonałym.

Średnia kwadratów prędkości cząsteczek w gazie doskonałym może być określona z definicji w skali temperatury T, tak aby:

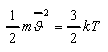 czyli

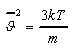
Stąd średnia kwadratu prędkości cząstek określona jest zależnością :

Średnia prędkość cząstek definiowana jest przez:

 

23. W przemianie izotermicznej masowa gęstość zasobu ciepła, praca techniczna są sobie równe:

wartość masowych gęstości zasobu ciepła wymienionego w przemianie izotermicznej

dqT = Td_r = pdV = -V²dp

 

24. Punkt krytyczny K:

Odpowiada stanowi krytycznemu, w którym objętościowe gęstości zasobu masy dwóch faz są jednakowe a przy zmianie stanu skupienia nie pojawia się powierzchnia podziału faz.

 

Przemiany termodynamiczne

 

25. Przemiana izochoryczna

26. Przemiana izobaryczna.

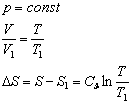
27. Przemiana izotermiczna.

28. Napisz wyrażenie określające funkcję rozkładu widmowego objętościowej gęstości zasobu ilości oscylatorów w polu długości fal pudła izotermicznego:

 

29. Napisz wyrażenie określające funkcję rozkładu widmowego objętościowej gęstości zasobu ilości oscylatorów w polu.

30. Sprawność internijna (wewnętrzna)

Nazywamy stosunek pracy (mocy) internijnej do pracy (mocy) obiegu porównawczego h_i=L_i/L_ob=N_i/N_ob

 

31. Sprawność efektywna

Nazywamy stosunek pracy (mocy) efektywnej do pracy (mocy) obiegu porównawczego h_e=L_e/L_ob=h_m*h_i

 

32. Sprawność termiczna

Nazywamy stosunek masowej gęstości zasobu pracy internijnej do wartości opałowej paliwa h_t=L_i/W_u

 

33. Sprawność termiczna obiegu porównawczego

Nazywamy stosunek pracy obiegu porównawczego do ciepła dostarczonego do obiegu h_ob.=L_ob/Q_d

 

34. Podaj definicję stopnia suchości pary mokrej.

x=m_p/(m_c+m_p) – jest udziałem masowym pary suchej nasyconej w mieszaninie cieczy i pary. Stopień suchości pary mokrej jest drugim, po ciśnieniu parametrem charakteryzującym stan pary mokrej.

Stopień suchości x może przyjmować wartości w zakresie od x=0, kiedy m_p=0 i mamy do czynienia tylko z cieczą wrzącą, do x=1 kiedy m_c=0 i mamy do czynienia tylko z para suchą nasyconą.

 

35. Zdefiniuj pojęcie wilgotności bezwzględnej gazu wilgotnego:

Wilgotność bezwzględna jest objętościową gęstością zasobu masy pary dla ciśnienia składnikowego dla pary ρ_p:

 

Max. wartość wilgotności bezwzgl. występuje wtedy, gdy ciśnienie pary jest równe ciśnieniu nasycenia dla danej temperatury:

 

36. Podaj zerową zasadę termodynamiki.

Jeżeli dwa układy nie graniczące ze sobą znajdują się w równowadze cieplnej z trzecim układem, z którym graniczą, to są one również w równowadze cieplnej między sobą.

 

37. I zasada termodynamiki

W odosobnionym układzie, tj. w układzie ciał który jest otoczony osłoną adiabatyczną wykluczającą jakąkolwiek wymianę energii z otoczeniem, całkowita energia w nim zawarta jest wielkością niezmienną. W układzie takim może zachodzić wzajemna przemiana jednego rodzaju energii w drugi, ale suma tych energii nie zmienia się.

 

38. I zasada termodynamiki dla ukł. otwartego:

Redukuje ona bilans zasobu energii wewnętrznej dla układu otwartego do warunków procesu termodynamicznie odwracalnego czyli do procesu termodynamicznego przebiegającego w warunkach równowagi termodynamicznej bez tarcia. Zatem zasada ta jest opisana równaniem:

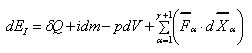
Jeżeli na układ bilansowania nie działają siły zewnętrzne to otrzymamy:

 

39. II zasada termodynamiki (Classiusa)

Żadna pracująca cyklicznie maszyna nie może, bez jakichś dodatkowych efektów, przenosić w sposób ciągły ciepła z jednego ciała do drugiego, mającego wyższą temperaturę.

 

40. II zasada termodynamiki (Kelvina (i Plancka))

Niemożliwa jest przemiana, której jedynym wynikiem byłaby zamiana na pracę ciepła pobranego ze źródła mającego wszędzie tę samą temperaturę.

 

 

41. Sformułuj II zasadę termodynamiki dla przemian nieodwracalnych:

W procesie nieodwracalnym iloczyn temp. bezwzględnej układu i elementarnego zasobu przyrostu entropii, równy jest sumie elementarnego przyrostu zasobu ciepła wymienionego między układem a otoczeniem, powiększonej o elementarny przyrost zasobu ciepła tarcia wykreowanego w układzie:

Tds = δQ + δQ_f

 

42. II zasada termodynamiki dla przemian odwracalnych.

W układzie nieadiabatycznym w procesie odwracalnym iloczyn temp. bezwzględnej T i elementarnego przyrostu zasobu entropii dS równy jest elementarnemu przyrostowi zasobu ciepła δQ wymienionego między układem a otoczeniem.

TdS = δQ.

W przemianach rzeczywistych nieodwracalnych przemianie termodynamicznej może towarzyszyć rozpraszanie energii w procesie tarcia, które jest równoważne kreacji zasobu ciepła Q_f.

dS = (dQ + dQ_f)/T

 

43. Napisz wnioski wynikające z II zas. termod.

Nie istnieje maszyna cieplna pracująca cyklicznie, wykonująca pracę bez zmian w otoczeniu:  ds = dQ/T

 

44. III zasada termodynamiki.

W pobliżu temperatury zera bezwzględnego suma entropii ciał reagujących przed reakcją jest taka sama jak po reakcji, tzn. że przyrost entropii związany z reakcją chemiczną zdąża do zera, czyli że w pobliżu temperatury T=0^oK entropia produktów reakcji jest równa entropii ciał wejściowych (substratów).

 

45. Sformułuj III zasadę termodynamiki dla przemian odwracalnych.

W układzie nie adiabatycznym w procesie odwracalnym iloczyn temperatury bezwzględnej układu i elementarnego przyrostu zasobu entropii, równy jest elementarnemu przyrostowi zasobu ciepła wymienionego między układem a otoczeniem. TdS=δQ

 

46. Podaj prawo Avogadra, wyjaśnij co określa liczba Avogadra.

W jednakowych objętościach znajduje się taka sama liczba cząstek tego samego gazu doskonałego jeśli ciśnienia i temperatury tych gazów są jednakowe: m₁=n₁•M₁,m₂=n₂•M₂ ; n – liczba cząstek gazu; M – masa cząsteczkowa; m – masa;

MR=B – uniwersalna stała gazowa.

Liczba Avogadra określa ilość cząstek zawartych w jednym molu dowolnej substancji. N_A=6,023•10²³[1/mol]

 

47. Wyjaśnij i zapisz prawo izochory Charles’a.

V,m = const   , a = 1/β = 273,15[K]

 ,

 ,

 

p = p₀(1+β₀t)

 

48. Równanie stanu gazu doskonałego Clapeyrona

Dokonując syntezy praw Boyle’a – Mariotta z prawem Gay – Lussaca dochodzi się do równania:

pV=MRT

 

49. Wyjaśnij prawo Daltona dla formy gazowej wieloskładnikowej

Ciśnienie całkowite „p” fazy gazowej wieloskładnikowej badanej mieszaniny gazów doskonałych, równoważne jest ciśnieniu jakie wywierałby gaz doskonały jednoskładnikowy mający następujące parametry stanu:

• temperaturę T równą temp. fazy gazowej wieloskładnikowej,

• objętościową gęstość zasobu ilości moli ρ_a równą sumie objętościowych gęstości zasobu ilości moli składników mieszaniny ρ_ni

50. Napisz wyrażenie definiujące temperaturę Debey'a

θ=hV_p/k

 

 

 

 

51. Wyjaśnij i zapisz zjawisko Joule’a – GayLussaca:

Opisuje ono dławienie adiabatyczno – izoenergetyczne gazu doskonałego. Podczas dławienia gazu następuje produkcja entropii jako, że jest to proces nieodwracalny i w stanie wyrównania ciśnień entropia układu osiąga max.

dS = δq_f/T =pdJ/T

Dla gazu doskonałego energia kinetyczna przemieszczenia substancjalnego cząsteczek po wyhamowaniu ich prędkości substancjalnej do zera równoważna energii cieplnej, równa jest co do wartości pracy bezwzględnej:  dq_f=pdJ

 

52. Wyjaśnij i zapisz prawo Gay-Lussaca:

Gazy rzeczywiste zbliżają swe wartości do gazu doskonałego wówczas gdy ciśnienie gazu maleje a temp. wzrasta i jest wysoka w porównaniu z temp. nasycenia

,

53. Podaj regułę faz Gibbsa:

p – liczba różnych faz,

c – liczba różnych składników,

f – liczba stopni swobody układu.

Reguła faz Gibbsa wskazuje, że dla zachowania równowagi powinien być spełniony warunek: f =c–p+2

Liczba stopni swobody to liczba takich parametrów jak: ciśnienie, temperatura i koncentracja składników układu, które mogą się zmieniać nie powodując naruszenia równowagi układu.

 

54. Napisz wyrażenie określające średnią energię oscylatora Plancka dla cząsteczki:

 

55. Prawo promieniowania Stefana

Strumień wymiany ilości cząstek odniesiony do jednostki powierzchni lub wymiana ilości cząstek przez jednostkę powierzchni w jednostce czasu, określany jest zależnością: n=nJ/4; n – objętościowa gęstość zasobu ilości cząstek gazu, J - prędkość średnia cząstek gazu. Natomiast przez analogię strumienia wymiany zasobu ilości fotonów określona jest zależnością nf=nc/4

R_T=sT⁴

 

56. Podaj prawo przesunięcia Viena.

λmT=hc/(k•4,965)=δ_w=2,898•10-3

Odwrotnie proporcjonalna zależność długości fal λm od temp. T opisuje ilościowo mechanizm przesuwania się maksimum rozkładu widmowego objętościowej gęstości zasobu energii promieniowania elektromagnetycznego ελ(λ) w miarę wzrostu temperatury w stronę fal krótszych.

 

57. Typowy wykres fazowy we współrzędnych (T,p) dla metalu:

T_tr – temp. punktu potrójnego

T_k – temp. punktu krytycznego

 równ. Clausiusa - Clapeyrona